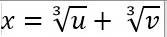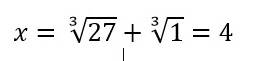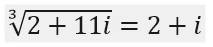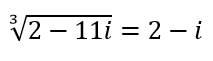ИСТОРИЧЕСКИЕ СВЕДЕНИЯ О РАЗВИТИИ АЛГЕБРЫ

М. Я. ВЫГОДСКИЙ

Вавилон. Истоки алгебры исходят к глубокой древности. Уже около 4000 лет назад вавилонские учёные владели решением квадратного уравнения и решали системы двух уравнений, из которых одно – второй степени. С помощью таких уравнений решались разнообразные задачи землемерия, строительного искусства и военного дела.

Буквенные обозначения, применяемые нами в алгебре, не употреблялись вавилонянами; уравнения записывались в словесной форме.

Диофант Александрийский 

Греция. Первые сокращённые обозначения для неизвестных величин встречаются у древнегреческого математика Диофанта (2 – 3 вв. н. э.). Неизвестное Диофант именует «аритмос» (число), вторую степень неизвестного – «дюнамис» (это слово имеет много значений: сила, могущество, имущество, степень и др¹.). Третью степень Диофант называет «кюбос» (куб), четвёртую – «дюнамодюнамис», пятую – «дюнамокюбос», шестую – «кюбокюбос». Эти величины он обозначает первыми буквами соответствующих наименований (ар, дю, кю, ддю, дкю, ккю). Известные числа для отличия от неизвестных сопровождаются обозначением «мо» (монас – единица). Сложение не обозначается совсем, для вычитания имеется сокращённое обозначение, равенство обозначается «ис» (исос – равный).

Ни вавилоняне, ни греки не рассматривали отрицательных чисел. Уравнение 3 ар 6 мо ис 2 ар 1 мо (3x + 6 = 2x +1) Диофант называет «неуместным». Перенося члены из одной части уравнения в другую, Диофант говорит, что слагаемое становится вычитаемым, а вычитаемое слагаемым.

  Китай. За 2000 лет до нашего времени китайские учёные решали уравнения первой степени и их системы, а также квадратные уравнения. Им были знакомы отрицательные и иррациональные числа. Так как в китайском письме каждый знак изображает некоторое понятие, то в китайской алгебре не могло быть «сокращённых» обозначений.

В последующие эпохи китайская математика обогатилась новыми достижениями. Так в конце 13 века китайцы знали закон образования биномиальных коэффициентов известных ныне под именем «треугольника Паскаля». В Западной Европе этот закон был открыт (Штифелем) на 250 лет позднее.

Индия. Индийские учёные широко применяли сокращённые обозначения неизвестных величин и их степеней. Эти обозначения являются начальными буквами соответствующих наименований (неизвестное называлось «столько-то»; для отличия второго, третьего и т. д. неизвестного употреблялись наименования цветов: «чёрное», «голубое», «жёлтое» и т. д.). Индийские авторы широко употребляли иррациональные² и отрицательные числа. Вместе с отрицательными числами в числовую семью вошёл нуль, который прежде обозначал лишь отсутствие числа.

Мухаммед аль-Хваризми (Хорезмиец). 

Страны арабского языка Узбекистан. Таджикистан. У индийских авторов алгебраические вопросы излагались в астрономических сочинениях; самостоятельной дисциплиной алгебра становится у учёных, писавших на международном языке мусульманского мира – арабском. Основоположником алгебры, как особой науки, нужно считать узбекского учёного Мухаммеда из Хорезма, известного под арабским прозвищем аль-Хваризми (Хорезмиец). Его алгебраический труд, составленный в 9 в. н. э., носит название «Книга восстановления и противопоставления». «Восстановлением» Мухаммед называет перенос вычитаемого из одной части уравнения в другую, где оно становится слагаемым; «противопоставлением» – собирание неизвестных в одну сторону уравнения, а известных – в другую сторону. По-арабски «восстановление» называется «ал-джебр». Отсюда название «алгебра».     

У Мухаммеда Хорезмского и у последующих авторов алгебра широко применяется к купеческим и иным денежным расчётам. Ни он, ни другие математики, писавшие по-арабски, не употребляли никаких сокращённых обозначений³. Они не признавали и отрицательных чисел: учение об отрицательных числах, знакомое им из индийских источников, они считали плохо обоснованным. Это было справедливо, но зато индийские учёные могли ограничиться одним случаем полного квадратного уравнения, тогда как Мухаммед Хорезмский и его приемники должны были различать три случая (x² + px = q, x² + q = px, x² = px + q; p и q – положительные числа).

аль-Бируни

Узбекские, таджикские, персидские и арабские математики обогатили алгебру рядом новых достижений. Для уравнений высших степеней они умели находить приближённые значения корней с очень большой точностью. Так, знаменитый узбекский философ, астроном и математик аль-Бируни (973 – 1048), родом также из Хорезма, свёл задачу о вычислении стороны правильного 9-угольника, вписанного в данную окружность, к кубическому уравнению x³ = 1 + 3x и нашёл (в 60-ричных дробях) приближённое значение x = 1,52' 45'' 47'''13'''' ⁴ (с точностью до ¹/₆₀⁴; в десятичных дробях это даёт семь верных десятичных знаков). Великий таджикский поэт и учёный Омар аль-Хайам (1048 – 1131) из Нишапура подверг систематическому изучению уравнения третьей степени. Ни ему, ни другим математикам мусульманского мира не удалось найти выражения корней кубического уравнения через коэффициенты. Но аль-Хайам разработал способ, по которому можно (геометрически) найти число действительных корней кубического уравнения (его самого интересовали только положительные корни).

Омар аль-Хайам (памятник в Иране)

Средневековая Европа. В 12 веке «Алгебра» аль-Хваризми стала известна в Европе и была переведена на латинский язык. С этого времени начинается развитие алгебры в европейских странах (сперва под сильным влиянием науки восточных народов). Появляются сокращённые обозначения неизвестных, решается ряд новых задач, связанных с потребностями торговли. Но существенного сдвига не было до 16 века. В первой трети 16 века итальянцы дель-Ферро и Тарталья нашли правила для решения кубических уравнений вида x³ = px + q; x³ + px = q; x³ + q = px, а Кардано в 1545 году показал, что всякое кубическое уравнение сводится к одному из этих трёх; в это же время Феррари, ученик Кардано, нашёл решение уравнения 4-й степени.

Людовик (Луиджи Феррари)

Джероламо Кардано 

Сложность правил для решения этих уравнений сделала необходимым усовершенствование обозначений. Это совершалось постепенно в течение целого столетия. В конце 16 века французский математик Виета ввёл буквенные обозначения, и при том не только для неизвестных, но и для известных величин (неизвестные обозначались заглавными гласными буквами, известные – заглавными согласными). Были введены сокращённые обозначения действий; у разных авторов они имели разный вид. В середине 17 века алгебраическая символика благодаря французскому учёному Декарту (1596 – 1650) приобретает вид, очень близкий к нынешней.

Франсуа Виет.

Жирар Альберт

Отрицательные числа. В 13 – 16 веках отрицательные числа рассматриваются европейцами лишь в исключительных случаях. После открытия решения кубического уравнения отрицательные числа постепенно завоёвывают право гражданства в алгебре, хотя их называют «ложными». В 1629 году Жирар (Франция) дал общеизвестный ныне способ изображения отрицательных чисел. Лет двадцать спустя отрицательные числа получили всеобщее признание.

Комплексные числа. Введение комплексных чисел также было связано с открытием решения кубического уравнения.

Николо Тарталья 

И до этого открытия при решении квадратного уравнения x² + q = px приходилось сталкиваться со случаем, когда требовалось извлечь квадратный корень из (^p/₂)² - q , где величина (^p/₂)² была меньше чем q. Но в таком случае заключали, что уравнение не имеет решений. О введении новых (комплексных) чисел в это время (когда даже отрицательные числа считались «сложными») не могло быть и мысли. Но при решении кубического уравнения по правилу Тартальи оказалось, что без действия над мнимыми числами нельзя получить действительный корень.

Объясним это подробнее. По правилу Тартальи корень уравнения

x³ = px + q             (1)

представляется выражением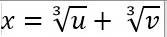

   (2)

где u и v – решение системы

u + v = q; uv = (^p/₃)³. (3)

Например, для уравнения x³ = 9x + 28 (p = 9; q = 28) имеем: u + v = 28; uv = 27,

откуда находим, что либо u = 27; v = 1, либо u = 1; v = 27.

 В обоих случаях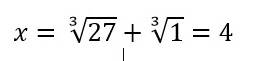 

Других действительных корней данное уравнение не имеет.

Но как заметил уже Кардано, система (3) может не иметь действительных решений, между тем как уравнение (1) имеет действительный и притом положительный корень. Так, уравнение x³ = 15x + 4 имеет корень x = 4, но система

u + v = 4; uv = 125

имеет комплексные корни: u = 2 + 11i, v = 2 -11i (или u = 2 – 11i, v = 2 + 11i).

На это загадочное явление впервые пролил свет Р. Бомбелли в 1572 г. Он указал, что 2 + 11i есть куб числа 2 + i, а 2 - 11i – куб числа 2 – i; значит можно написать 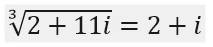; 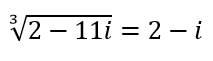, и тогда формула (2) даёт x = (2 + i) + (2 - i) = 4.

Леонард Эйлер 

С этого момента нельзя было игнорировать комплексные числа. Но теория комплексных чисел развивалась медленно: ещё в 18 веке крупнейшие математики мира спорили о том, как находить логарифмы комплексных чисел. Хотя с помощью комплексных чисел удалось получить много важных фактов, относящихся к действительным числам, но самое существование комплексных чисел многим казалось сомнительным. Исчерпывающие правила действия с комплексными числами дал в середине 18 века русский академик Эйлер – один из величайших математиков всех времён и народов. На рубеже 18 и 19 веков было указано Весселем (Дания) и Арганом (Франция⁵) геометрические изображения комплексных чисел. Но на работы Весселя и Аргана не обратили внимания, и лишь в 1831 г., когда тот же способ был развит великим математиком Гауссом (Германия), он стал всеобщим достоянием.

Каспар Вессель

Жан Робер Арган

Вслед за тем как были решены уравнения 3-й и 4-й степени, математики усиленно искали формулу для решения уравнения 5-й степени. Но Руффини (Италия) на рубеже 18 и 19 веков доказал, что буквенное уравнение пятой степени x⁵ +ax⁴ + bx³ + ex² + dx + e = 0 нельзя решить алгебраически; точнее: нельзя выразить его корень через буквенные величины a, b, c, d, e с помощью шести алгебраических действий (сложение, вычитание, умножение, деление, возведение в степень, извлечения корня⁶).

В 1830 г. Галуа (Франция) доказал, что никакое общее уравнение, степень которого больше, чем 4, нельзя решить алгебраически.

Тем не менее всякое уравнение n-й степени имеет (если рассматривать комплексные числа) n корней (среди которых могут быть и равные). В этом математики были убеждены ещё в 17 веке (основываясь на разборе многочисленных частных случаев), но лишь на рубеже 18 и 19 веков теорема была доказана Гауссом.

Вопросы, которыми занимались алгебраисты 19 и 20 веков, по большей части выходят за пределы элементарной математики. Поэтому укажем только, что в 19 веке были разработаны многие методы приближённого решения уравнений. В этом направлении важные результаты были получены великим русским математиком Н. И. Лобачевским.      

¹На арабский язык термин «дюнамис» был переведён словом «маль», обозначающим «имущество». Западноевропейские математики в 12 веке перевели термин «маль» на латинский язык равнозначным словом census. Термин «квадрат» вошёл в употребление лишь в 16 веке.

²Греческие математики умели находить приближённые значения корней, но в алгебре старались избегать иррациональностей.

³В них не было и нужды, ибо арабское письмо очень кратко: гласные не обозначаются, согласные и полугласные буквы просты по начертанию и сливаются по нескольку в один знак. Для написания многих слов требуется не больше времени, чем для написания некоторых наших букв (например, ж, ш). Зато арабская грамота много труднее нашей.

⁴Т. е. одна целая, 52 шестидесятых, 45 три тысячи шестисотых и т. д.

⁵Первые шаги в этом направлении были сделаны Валлисом (Англия) в 1685 г.  

⁶В доказательстве Руффини были некоторые недочёты. В 1824 г. Абель (Норвегия) дал безупречное доказательство.